Zanim jednak powiemy czym jest jakość indeksu, musimy zdefiniować pojęcia fundamentalne i porównać metody odczytu danych poprzez Index Table Access (ITA) i tzw. Full Table Scan (FTS)

Porównanie ITA i FTS

Na początek załóżmy tabelkę z jednym indeksem na kolumnie unikalnej i zasilmy ją 10 mln rekordów.

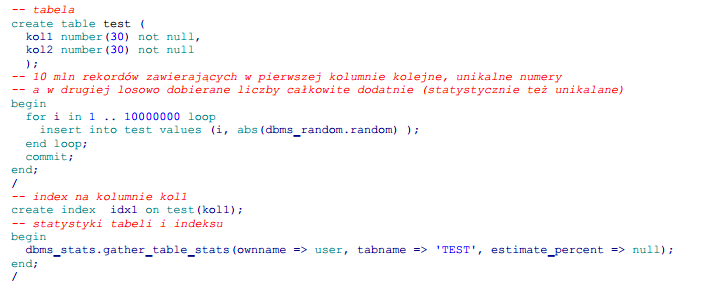
Spróbujmy zamodelować powyższą sytuację na prostym rysunku.

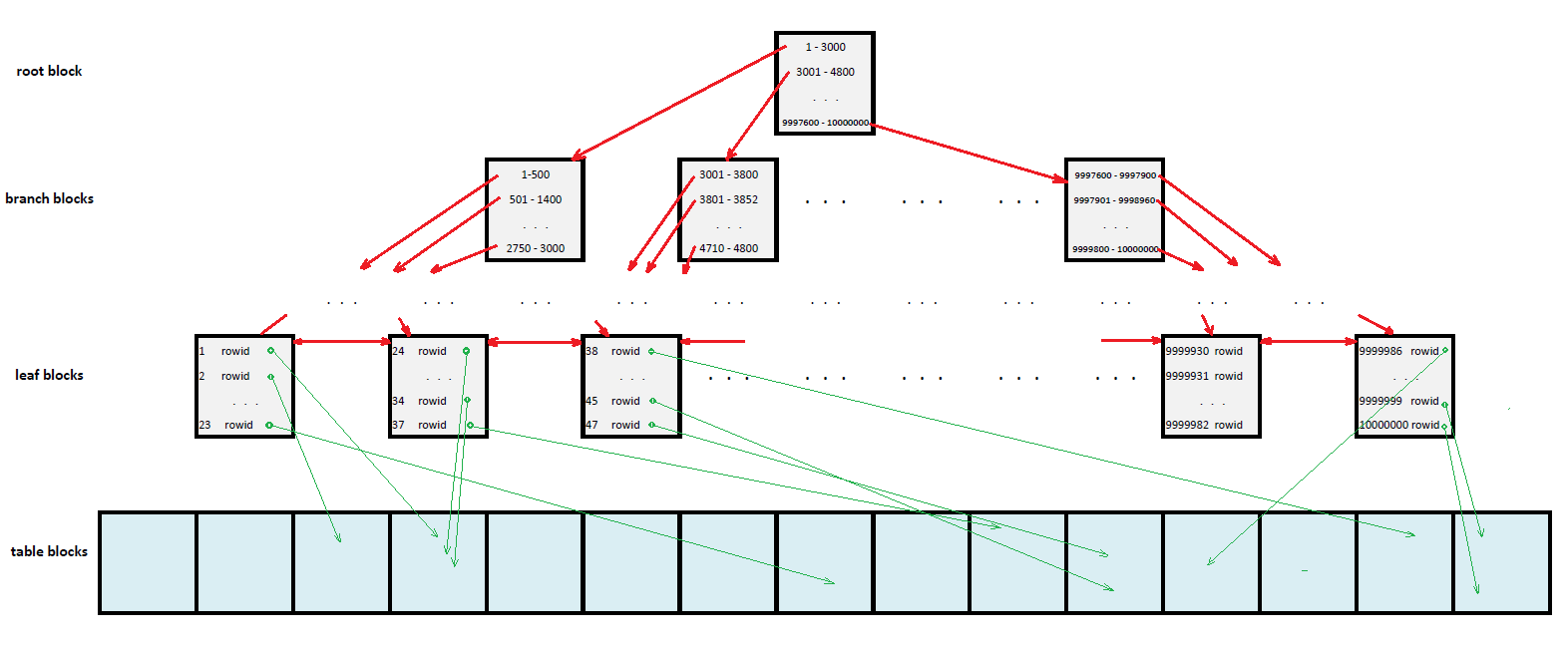
Tabela jest tutaj sekwencją niebieskawych bloków, z których każdy zawiera (w zależności od długości wiersza) nawet kilkaset rekordów. Pełny odczyt tabeli (TFS) będzie polegał na sekwencyjnym przejrzeniu każdego bloku i odfiltrowaniu pożądanych rekordów. Koszty będą zatem proporcjonalne do liczby bloków (rozmiaru tabeli) niezależnie od liczby odnalezionych rekordów –  nawet jeśli w bloku niczego nie znajdziemy i tak ponieśliśmy koszty przeglądania.

Na zamieszczonym powyżej uproszczonym modelu indeksu B-Tree widać, że w bloku korzenia zapisane zostały równoliczne przedziały wartości występujących w indeksowanej kolumnie (liczba przedziałów zależy od jej objętości). Przy każdym przedziale znajduje się wskazanie (czerwona strzałka) na kolejny poziom indeksu (gałęzi), w którym przedziały te są zawężane. Sytuacja powtarza się dopóty, dopóki przedziały nie będą zawierały wystarczająco mało wartości aby można je było wyliczyć w jednym bloku (liść). Przy każdej wartości w bloku liścia  mieści się ROWID wiersza zawierającego zadaną wartość w kolumnie indeksowanej. Pozwala  on określić, gdzie dokładnie w tablicy (pliku, bloku, pozycji w bloku) jest poszukiwany rekord (zielona strzałka).

Przy okazji rekurencyjnego zawężania przedziałów klucze w indeksie zostały posortowane. Można to wykorzystać „chodząc” po indeksie nie tylko z góry na dół, ale również w lewo i prawo przy pomocy dwukierunkowej listy powiązań (czerwone poziome strzałki na poziomie liści).

Aby porównać koszty ITA i TFS, naszkicujmy dwa wykresy.

1. Zależność kosztu odczytu rekordu (pojedynczego) od wielkości tabeli

Przeprowadźmy teraz drobny eksperyment myślowy.

TFS –  Jeśli tabela jest mała, mamy niewiele bloków do sprawdzenia; jeśli natomiast jest duża, musimy przejrzeć ich dużą liczbę. Dwa razy większa tabela to dwa razy więcej bloków i dwa razy większy koszt  -zależność kosztu od wielkości jest więc liniowa.

ITA –  Jeśli szukamy rekordu o konkretnej wartości indeksowanego klucza, wchodzimy w korzeń, następnie dobieramy przedział, przechodzimy do kolejnego poziomu i do jeszcze kolejnego, aż w liściu odnajdujemy ROWID. Możemy teraz odczytać z tabeli poszukiwany rekord; koszty jego odczytu zależą więc od głębokości drzewa indeksu. A jak głębokość indeksu ma się do rozmiaru tabeli? Załóżmy, że w jednym bloku zaadresujemy 1000 rekordów tabeli. Drugi poziom musi powstać, gdy tabela przekroczy 1000 rekordów. Trzeci poziom powstanie,  kiedy osiągnie 1000×1000 rekordów ( prawie milionowy przyrost), czwarty przy wyniku 1000x1000x1000 rekordów ( prawie miliardowy przyrost), piąty gdy przekroczy tysiąc miliardów, itd…

Wprawdzie w jednym bloku nie zmieścimy tysiąca przedziałów, warto jednak zauważyć logarytmiczną zależność między liczbą poziomów drzewa a rekordów w tabeli. Nieco upraszczając, jeśli pominiemy nieszczególnie nas interesujące tabele małe, możemy założyć, że głębokość drzewa jest stała i niezależna od   liczby rekordów w tabeli. Koszt znalezienia rekordu (oczywiście pomijając małe nieistotne tabele) jest zatem stały i nie zależy od rozmiaru tabeli.

Im indeksowana kolumna jest większa w bajtach, tym głębokość drzewa indeksu może być większa, ale niezależnie od jej objętości dochodzimy do poziomu, na którym drzewo się stabilizuje i nie pogłębia dalej. Przy okazji – głębokość drzewa minus jeden znajdą Państwo w statystyce indeksu BLEVEL.

Nanieśmy wyniki naszej analizy na wykres pamiętając, że dotyczy on jednego rekordu.

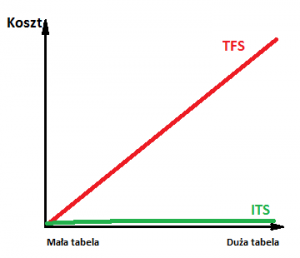
2. Zależność kosztu odczytu od ilości szukanych rekordów (w dużej tabeli)

TFS – Jeśli tabela jest duża, musimy przejrzeć wszystkie jej bloki niezależnie od tego czy szukamy jednego rekordu, czy wszystkich; koszt nie zależy więc od  liczby poszukiwanych rekordów. Potwierdźmy to na naszej tabeli testowej:

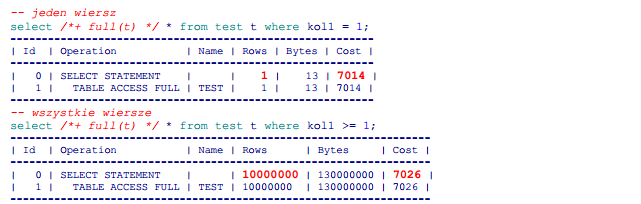
ITA –Wiemy już z poprzedniego wykresu, że jeśli szukamy jednego rekordu, koszt jest stały i bliski zeru. Sprawdźmy, jak się kształtuje koszt przy poszukiwaniu 10000, 20000, 30000 czy w skrajnym wypadku 10 milionów rekordów.

Wyniki dla zapytania

zamieściłem w poniższej tabelce:

Można tu odczytać, że koszt używania indeksu zależy liniowo od liczby poszukiwanych indeksem rekordów. Dałoby się nawet wyliczyć koszt przypadający na jeden poszukiwany rekord – najpierw mamy pewien koszt stały wynikający z wędrówki po indeksie od korzenia do liścia ( cztery jednostki na pierwszy wiersz). Następnie idziemy po liściach w lewo od znalezionej wartości granicznej i skaczemy do tablicy do namierzonych w indeksie rekordów – każdy skok to dodatkowy koszt.

Spróbujmy nanieść nasze wyniki na wykres pamiętając, że analizujemy dużą tabelę:

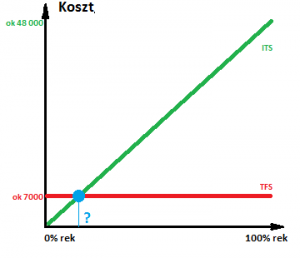
Możemy stąd wyciągnąć bardzo interesujący wniosek – z indeksów opłaca się korzystać tylko do pewnej  liczby szukanych rekordów. Powyżej pewnego progu indeksy nie tylko nie pomagają, ale stosowane nieodpowiednio do sytuacji potrafią też sporo zaszkodzić.

Przyszła pora na kwestię kluczową  – przy ilu procentach rekordów przestaje nam się opłacać używanie indeksów? Gdzie znajduje się punkt zaznaczony na wykresie niebieskim pytajnikiem? Zdajmy się na CBO i metodą kolejnych prób znajdźmy maksymalną  liczbę rekordów, dla której optymalizator będzie jeszcze chciał używać indeksu:

Bazując na powyższym planie, możemy obliczyć procentowy próg opłacalności korzystania z naszego indeksu:

Potrafimy już porównać nasz indeks z pełnym odczytem – pora na przejście do sedna, czyli jakości..

Dobre i złe indeksy

Aby porównywać indeksy, musimy mieć co najmniej dwa. W związku z tym załóżmy na naszej tabeli drugi indeks na kolumnę kol2, uzupełnijmy analogiczną tabelkę z kosztami i narysujmy wykres dla tego indeksu.

Od razu tu widać, że indeksy zachowują się zupełnie inaczej; wprawdzie nadal występuje stała wartość początkowa dla jednego rekordu, ale potem każde kolejne 10 tys. kosztuje już nie 49 jednostek kosztu, tylko ponad 10 000. Dla wszystkich rekordów daje to oszałamiającą wartość grubo ponad 10 mln kosztu.

Nanieśmy drugi indeks na wykres:

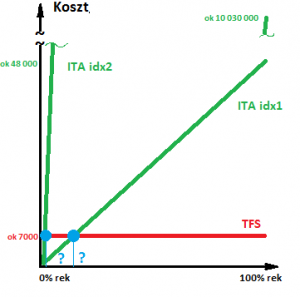
Jak teraz prezentuje się próg opłacalności korzystania z indeksu?

Bazując na powyższym planie możemy obliczyć procentowy próg opłacalności korzystania z naszego indeksu:

Dwa indeksy na tej samej tablicy, a tak bardzo się od siebie różnią! Drugi ma 200 razy mniejszy próg opłacalności; w pierwszym 10 tys. wierszy dostaniemy w cenie ok 50 jk, w drugim natomiast będzie to aż 10 000 jk za każde 10 tys. wierszy.

Możemy teraz jasno wskazać od czego zależą koszty poszukiwania rekordów indeksem – jest to iloczyn pewnego jednostkowego kosztu i liczby poszukiwanych wierszy.

koszt odnalezienia rekordów = koszt jednostkowy pobrania wiersza *  liczba wierszy

To właśnie ten jednostkowy koszt (na wykresie wyrażony nachyleniem prostej indeksu), czyli cena, którą musimy zapłacić za jeden wiersz będzie definiował jakość indeksu.

Możemy teraz na chwilę wrócić do twierdzenia od którego rozpoczął się ten artykuł; dobre indeksy to te na unikalnej kolumnie, a złe na kolumnie z małą ilością wartości. Jeżeli nasz indeks jest unikalny, to pytając o konkretną wartość klucza dostajemy jeden rekord – a więc niezależnie od jakości mamy minimalne koszty zależne tylko od głębokości drzewa. Jeśli natomiast mamy kolumnę z trzema różnymi wartościami, w każdym wypadku otrzymamy 1/3 rekordów, a indeks nie będzie się nadawać bez względu na jakość ( Chyba, że wartości nie będą równomiernie dystrybuowane, ale to już temat na zupełnie inny artykuł).

W drugiej części opowiem skąd biorą się takie rozbieżności, jak je zmierzyć i – co najważniejsze – jak poprawić szczególnie dla nas ważny indeks.