Dzień dobry.
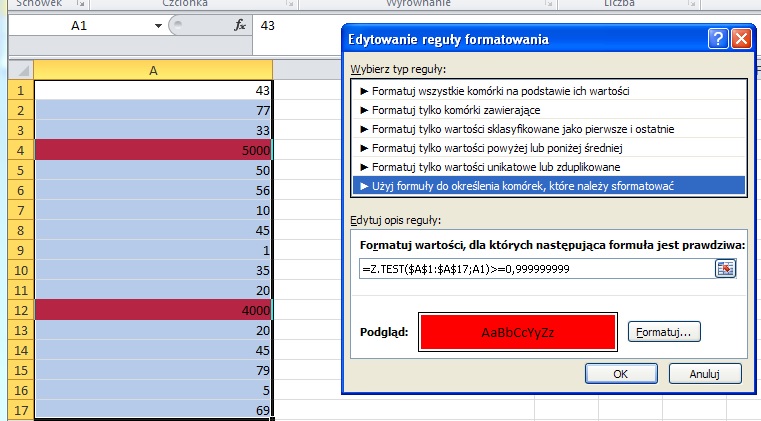
Jak wyznaczyć/wyliczyć outliersy w Accessie lub Excelu. Mam tabelę z polami: produkt, lokalizacja, cena. Potrzebuję wyznaczyć/znaleźć ceny, które znacząco odbiegają od pozostałych w ramach każdego produktu wśród kilkudziesięciu lokalizacji, przy czym mogą zdarzyć się sytuację, że dla jakiejś lokalizacji może nie być ceny. Czy ma ktoś jakiś pomysł?
Na razie próbowałem w Excelu za pomocą mediany i odchylenia standardowego, ale rezultat nie jest taki jaki oczekiwałem.
W załączniku przykład z formatowaniem warunkowym - suwakiem ustawiamy czułość. Im suwak wyżej - tym więcej wartości traktowanych jest jako outliers. Im suwak niżej - tym tolerancja jest mniejsza i mniej wartości kwalifikuje się jako wyjątki. Proszę zwrócić uwagę na formułę w regule formatowania warunkowego:
=ABS($A1-AVERAGE($A$1:$A$25))>$F$1*STDEV($A$1:$A$25)
(w wersji polskiej Excela ABS to MODUŁ.LICZBY, AVERAGE to ŚREDNIA, a STDEV to ODCH.STANDARDOWE, czyli:
=MODUŁ.LICZBY($A1-ŚREDNIA($A$1:$A$25))>$F$1*ODCH.STANDARDOWE($A$1:$A$25)
Formuła ta sprawdza, czy liczba oddalona jest na osi liczbowej od wartości środkowej (czyli średniej) o więcej niż wartość odchylenia standardowego (czyli średniego odchylenia) przemnożonego przez czynnik oznaczający czułość (tutaj to komórka $F$1). Ustawienie komórki $F$1 na wartość większą niż 1,5-2 wyłapuje już dość dobrze wyjątki (oczywiście wszystko zależy od natury problemu!).
Załączniki
Witam.
W takim wypadku zaproponowałbym zastosowanie funkcji Z.TEST()
Sprawdza jakie jest prawdopodobieństwo czy średnia z wybranej próbki jest większa od średniej dla zbioru
Można połączyć to z formatowaniem warunkowym dla ciekawszego efektu:
Celowo nie przyrównuje wyniku testu Z do 1 (czyli 100% prawdopodobieństwo), żeby uniknąć nie objęcia wartości zbliżających się do 1.
Pozdrawiam.
I zapraszam po więcej takich ciekawych wyliczeń na szkolenie EXbiz
Pozdrawiam.
Tomasz Grabowski
Zgodzę się z przedmówcą. Podobny efekt można uzyskać przeliczając wyniki na skalę Z z użyciem formuły NORMALIZUJ. Wtedy uzyskujemy wyniki na skali, której średnia wynosi 0 a odchylenie standardowe 1. Każdy z wyników zmienia nam się w wartość, która wyraża odległość wyniku od średniej w jednostce odchylenia standardowego.
Interpretacja: wartości powyżej 3 odchyleń oraz mniejsze od -3 wymagają naszej uwagi, szczególnie jeśli jest ich więcej niż 0,1%. To może wskazywać na zniekształcenia rozkładu i nadreprezentację skrajnych wartości. Wartości powyżej 3 i poniżej -3 możemy traktować jako przypadki nietypowe/odstające.
A tu dlaczego akurat 3/-3 odchylenia standardowe (poniżej 1% traktowane jako wyjątki):
Uzupełniając jeszcze niniejszą dyskusję. Funkcja Z.TEST domyślnie jako trzeci parametr (sigma) bierze odchylenie standardowe. To nieco za mało w wielu sytuacjach na potraktowanie wartości jako odstającej. Przykład: lista pensji pracowników, rozkład normalny, średnia 3200, odchylenie standardowe 800. Dla około 100 pensji lista zawiera pensje od ok. 900 do ok. 5400 zł (w rozkładzie normalnym). Funkcja Z.TEST z pominiętym parametrem sigma traktuje już pensję 3800 jako odstającą. Mimo, że jeszcze ponad ok. pracowników (ze 100) ma pensję powyżej tej. Dużo lepiej to wygląda przyjmując jako sigma 3*ODCH.STANDARDOWE(zakres). Wtedy tylko 2-3 najwyższe pensje traktowane są jako odstające (powyżej 4900 zł).
Należy również bardzo uważać, ponieważ z symetrii rozkładu wynika, że podobnie będzie z pensjami najniższymi (też będzie kilka odstających), a funkcja Z.TEST ich nie pokaże! Tu rozwiązaniem jest policzenie Z.TEST np. dla odwrotności pensji. Wtedy pensje poniżej ok. 1700 wskazywane są jako odstające (przy założenie sigma=3*ODCH.STANDARDOWE(zakres)).
W załączniku przykładowy plik z rozwiązanie powyższego problemu.
Załączniki
Dorzucę jeszcze jedną rzecz, nie zawsze trzeba unikać przypadków odstających. Raczej powinniśmy zadać sobie pytanie czy nie jest ich zbyt dużo. Ich ilość wynika z krzywej normalnej, jeśli na 1 000 przypadków trafi nam się 1 powyżej 3SD to jest to wartość, której należy się spodziewać. Jeśli trafi ich się 10, to jest ich zbyt wiele, ponieważ powyżej 3 SD w rozkładzie normalnym znajdziemy tylko 0,1% przypadków
Jako kontynuację tej dyskusji chciałbym zapytać szanowne Koleżanki i Kolegów, co zrobić w następujących przypadkach? Jak wtedy wyznaczyć wartości/przypadki odstające, lub sprawdzić czy nie jest ich zbyt dużo:
1) dla rozkładów innych niż normalne,
2) w sytuacji wielowymiarowej, tzn. gdy przypadki to nie wartości skalarne, ale całe rekordy (mające kilka cech),
3) gdy nie ma rozkładu, np. dla szeregów czasowych,
4) gdy na pierwszy rzut oka dane wyglądają chaotycznie i nie da się ich wpasować w powyższe przypadki (ale może da się wyznaczyć punkty skupienia/grupy przypadków i odstające to będą te, które nie leżą "w zasięgu" żadnej grupy)?
Tę dyskusję przenoszę do innego wątku: https://quorum.akademiq.pl/discussion/1347/jak-wyznaczyc-warto%C5%9Bciprzypadki-odstajace-w-ponizszych-sytuacjach
@ Piotr Piątek
@ 1.
Użyć innych rozkładów w zależności od tego jak wyglądają dane. Oczywiście będzie to wymagało transformacji danych na inną skalę, jednak da nam te same informacje co w przypadku krzywej normalnej. Inne popularne rozkłady:
